Tiempo de lectura estimado: 8 minutos
Calor diferencial de disolución
El Calor Diferencial de Disolución (CDD) es una propiedad termodinámica que describe la variación de energía térmica asociada con la disolución de 1 mol de soluto en relación con la concentración de la disolución. Durante el proceso de disolución, la cantidad de calor absorbido o liberado por mol de soluto no es constante, sino que exhibe una dependencia significativa de la concentración del soluto en la disolución.
Este fenómeno se manifiesta como una absorción o liberación de calor durante el proceso de disolución de una sustancia. Este calor, al referirse a un mol de sustancia en cualquier punto del proceso, es denominado Calor Diferencial de Disolución. Es importante destacar que esta magnitud no permanece constante, sino que experimenta variaciones en función de la cantidad de disolvente presente y, en consecuencia, de la concentración de la disolución resultante.
Al disolver gradualmente una masa específica de sustancia en una cantidad determinada de disolvente, la composición de la disolución experimenta cambios desde la del disolvente puro hasta alcanzar la composición final de la disolución.
En este proceso, el Calor Diferencial de Disolución se manifiesta como una medida dinámica que refleja la variación de energía térmica asociada con la concentración cambiante de soluto en la disolución, proporcionando así una descripción más detallada y precisa de los aspectos termodinámicos involucrados en el proceso de disolución química.
La siguiente expresión modela el calor diferencial de disolución
$\left|\frac{\partial(\Delta H)}{\partial n}\right|_{p, T}$
Calor integral de disolución
El Calor Integral de Disolución se define como la variación de entalpía que ocurre al disolver una cantidad específica de soluto en una determinada cantidad de disolvente. La variación total de calor, expresada por mol de soluto, al finalizar el proceso de disolución, constituye el Calor Integral de Disolución. Este parámetro termodinámico experimenta variaciones en función del número de moles de disolvente en los cuales el soluto ha sido disuelto.
Cuando la cantidad de disolución es tan extensa que cualquier dilución adicional no induce cambio alguno en el calor liberado o absorbido, se introduce el subíndice (aq) en la ecuación termoquímica para denotar una solución acuosa. Un ejemplo ilustrativo de este comportamiento se observa comúnmente al mezclar ácido sulfúrico con una gran cantidad de agua, y este fenómeno puede ser descrito mediante una ecuación termoquímica.

En particular, el Calor Integral de Solución se refiere al cambio de entalpía cuando 1 mol de soluto se mezcla con una cantidad fija de solvente puro. Así, el Calor Integral de Solución está intrínsecamente vinculado a la cantidad de solvente presente o corresponde a una concentración específica en la disolución resultante. Esta relación detallada del Calor Integral de Disolución con la concentración y cantidad de solvente proporciona una comprensión más profunda de los aspectos termodinámicos involucrados en el proceso de disolución química.
No obstante, resulta más intrigante conocer la cantidad total de calor absorbido o liberado por mol de sustancia durante el proceso completo, es decir, cuando se disuelve la totalidad de la sustancia en la cantidad predeterminada de disolvente. La magnitud de calor generada bajo estas condiciones se expresa mediante:
Es fundamental establecer una distinción entre el Calor Integral de Solución y el Calor Integral de Dilución. Este último representa la variación de entalpía durante la dilución de 1 mol de soluto con el mismo solvente puro, transcurriendo desde una concentración a otra. Se define como la diferencia entre los Calores Integrales de cada una de las concentraciones consideradas.
En el límite en el cual la fracción molar del solvente tiende a 1, se obtiene el Calor Integral de Soluto a Dilución Infinita (ΔH°), equivalente al calor absorbido por el sistema cuando 1 mol de soluto se disuelve en una cantidad infinita de solvente, manteniendo constantes la temperatura (T) y la presión (P).
Experimentalmente, se observa que la entalpía integral de solución (ΔHint) es dependiente de la temperatura (T), la presión (P) y la composición molar (α) para una mezcla de dos componentes: un soluto y un solvente. Esta dependencia se expresa mediante la ecuación:
\[ \Delta H_{\text{int}} = \Delta H (T, P, n_1, n_2) \]
Donde \(\Delta H_{\text{int}}\) representa la entalpía integral de solución, y la función \(\Delta H (T, P, n_1, n_2)\) describe la variación del calor integral con respecto a la temperatura, presión y la composición molar de la mezcla.
La expresión total de la diferencia, representada por la derivada total de la entalpía integral \(\Delta H_{\text{int}}\), se describe mediante:
\[ \frac{d \Delta H_{\text{int}}}{dt} = \left( \frac{\partial H}{\partial T} \right)_{P, n_1, n_2} \frac{dT}{dt} + \left( \frac{\partial H}{\partial P} \right)_{T, n_1, n_2} \frac{dP}{dt} + \left( \frac{\partial H}{\partial n_1} \right)_{T, P, n_2} \frac{dn_1}{dt} + \left( \frac{\partial H}{\partial n_2} \right)_{T, P, n_1} \frac{dn_2}{dt} \]
Donde:
– \( \left( \frac{\partial H}{\partial T} \right)_{P, n_1, n_2} \) es la derivada parcial de la entalpía con respecto a la temperatura a presión constante y con moles de soluto y solvente dados.
– \( \left( \frac{\partial H}{\partial P} \right)_{T, n_1, n_2} \) es la derivada parcial de la entalpía con respecto a la presión a temperatura constante y con moles de soluto y solvente dados.
– \( \left( \frac{\partial H}{\partial n_1} \right)_{T, P, n_2} \) y \( \left( \frac{\partial H}{\partial n_2} \right)_{T, P, n_1} \) son las derivadas parciales de la entalpía con respecto a los moles de soluto y solvente, respectivamente, a temperatura y presión constantes, y con la cantidad de la otra sustancia dada.
Este resultado es válido para un proceso a temperatura (T) y presión (P) constantes.
La expresión de la derivada total de la entalpía integral \(\frac{d \Delta H_{\text{int}}}{dn}\) se desarrolla como:
\[ \frac{d \Delta H_{\text{int}}}{dn} = \frac{\Delta H_1}{n_1} + \frac{\Delta H_2}{n_2} \]
Donde:
\[ \Delta H_1 = \left( \frac{\partial H}{\partial n_1} \right)_{T, P, n_2} \]
\[ \Delta H_2 = \left( \frac{\partial H}{\partial n_2} \right)_{T, P, n_1} \]
En la termodinámica, se demuestra que esta ecuación es equivalente a:
\[ \Delta H_{\text{int}} = \Delta H_1 + \Delta H_2 \]
Donde \(\Delta H_1\) y \(\Delta H_2\) representan los calores diferenciales o las entalpías molares parciales de solución del soluto y solvente, respectivamente. Estas son funciones de la temperatura (T), la presión (P), y la composición de la solución.
El calor diferencial de solución se refiere a una situación en la cual se mide el incremento de entalpía cuando un mol de solvente o soluto se disuelve en un volumen tan extenso de solución que no se produce un cambio apreciable en la concentración.
La curva característica que representa la variación del calor integral de 1 mol de soluto (\(n_2 = 1\), constante) en un solvente (\(n_1\)) es una herramienta útil para comprender la relación entre el calor de solución y la composición de la mezcla.
Materiales
- Probeta graduada de 10 ml o pipeta graduada de 10 ml
- Thermo, Calorímetro o frasco Dewar
- Termómetro o Sensor de temperatura (preferible)
- Cronometro
- Pipeteador o propipeta (si se va a emplear pipeta)
Reactivos
- Agua destilada
- Solución de ácido sulfúrico al 98%
- Solución de nitrato de amonio al 99%
- Solución de nitrato de amonio 10N
Procedimiento – Calor diferencial e integral de disolución
Se dispone de un termo o frasco Dewar que contiene 150 ml de agua destilada a temperatura ambiente.
Posteriormente, se añade una cantidad específica de soluto ácido sulfúrico (H2SO4) concentrado, permitiendo que se establezca el equilibrio durante 4 minutos. Se registra la temperatura en este punto.
El experimento se repite utilizando la misma cantidad de soluto hasta alcanzar el volumen indicado en la siguiente tabla.
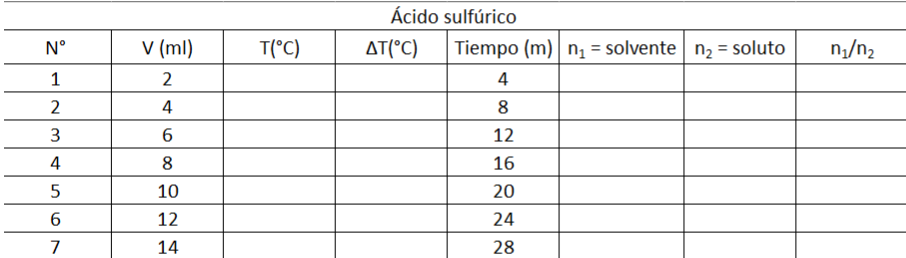
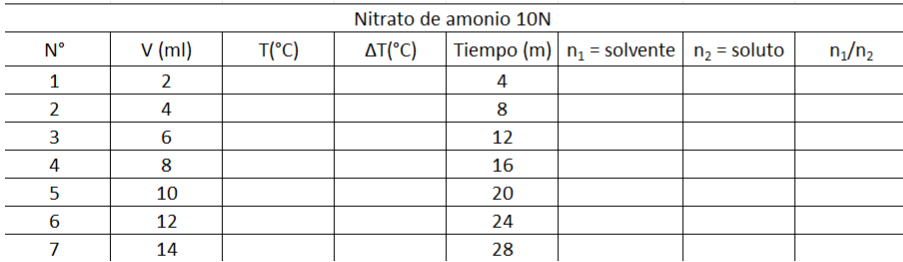
La misma operación se lleva a cabo para el soluto nitrato de amonio (NH4NO3) al 99% de pureza y para el nitrato de amonio de concentración 10N
Tabla para el nitrato de amonio 99%

Tabla para el nitrato de amonio 10 N
Después del laboratorio
Para cada ensayo realice un gráfico de temperatura T versus el tiempo y determine su pendiente media. También realice una tabla de datos de T (°C), ΔT(°C) y tiempo (min).
Donde C es la capacidad calorífica del termo o frasco Dewar. En caso de no tener este valor se puede asumir como C = 22.26998 Cal/°C ≈ 592.7564 J/K.
Igualmente, elabore la gráfica de ΔHint vs. n1/n2 (donde n1 es el número de moles de agua y n2 es el número de moles de ácido sulfúrico), así como para las dos concentraciones de hidróxido de amonio.
Como citar este artículo:
APA: (2024-02-14). Calor diferencial e integral de disolución. Recuperado de https://quimicafacil.net/manual-de-laboratorio/fisicoquimica/calor-diferencial-e-integral-de-disolucion/
ACS: . Calor diferencial e integral de disolución. https://quimicafacil.net/manual-de-laboratorio/fisicoquimica/calor-diferencial-e-integral-de-disolucion/. Fecha de consulta 2026-02-13.
IEEE: , "Calor diferencial e integral de disolución," https://quimicafacil.net/manual-de-laboratorio/fisicoquimica/calor-diferencial-e-integral-de-disolucion/, fecha de consulta 2026-02-13.
Vancouver: . Calor diferencial e integral de disolución. [Internet]. 2024-02-14 [citado 2026-02-13]. Disponible en: https://quimicafacil.net/manual-de-laboratorio/fisicoquimica/calor-diferencial-e-integral-de-disolucion/.
MLA: . "Calor diferencial e integral de disolución." https://quimicafacil.net/manual-de-laboratorio/fisicoquimica/calor-diferencial-e-integral-de-disolucion/. 2024-02-14. Web.
Si tiene alguna pregunta o sugerencia, escribe a administracion@quimicafacil.net, o visita Como citar quimicafacil.net
